
有理数,这一数学概念,在数学领域占据了极其重要的地位。它不仅在日常计算中频繁出现,也是进一步学习数学和其他科学领域知识的基础。那么,有理数到底是什么意思呢?哪些数又属于有理数的范畴呢?接下来,我们将从定义、表现形式、实例以及有理数在数轴上的表示等多个维度,来深入解析有理数这一概念。
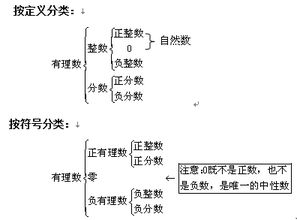
有理数,简而言之,是可以表示为两个整数之比的数。具体地说,如果一个数可以写成a/b(a和b都是整数,且b不为0)的形式,那么这个数就是有理数。这个定义中的“有理”一词,源于古希腊数学家毕达哥拉斯学派的一个观念,他们认为只有可以表示为整数比的数才是真实存在的、合理的数,而那些无法表示为整数比的数(如无理数)则被认为是不可理解的。
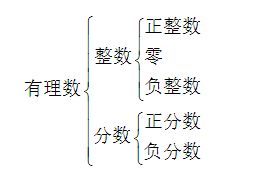
有理数有多种表现形式,其中最常见的是分数形式和十进制小数形式。

1. 分数形式:如前所述,有理数可以表示为两个整数的比,即a/b(a,b∈Z,b≠0)。例如,1/2、3/4、-5/6等都是有理数。

2. 十进制小数形式:有理数还可以表示为有限小数或无限循环小数。有限小数如0.5(等于1/2)、1.25(等于5/4)等;无限循环小数如0.333...(等于1/3)、0.142857142857...(等于1/7)等。需要注意的是,虽然有些无限不循环小数在数学中也占据重要地位(如π、e等),但它们并不属于有理数的范畴,而是被称为无理数。
为了更直观地理解有理数的概念,我们可以列举一些具体的实例。
1. 整数:所有的整数都是有理数,因为整数可以看作是分母为1的分数。例如,5可以表示为5/1,-3可以表示为-3/1。
2. 有限小数:如前所述,有限小数都是有理数。例如,0.25(等于1/4)、0.75(等于3/4)、1.6(等于8/5)等。
3. 无限循环小数:无限循环小数也是有理数。例如,0.333...(等于1/3)、0.1666...(等于1/6,虽然这里只展示了三位循环,但实际上它是无限循环的)、0.090909...(等于1/11)等。
4. 分数:除了整数和有限小数外,分数本身也是有理数的一种表现形式。例如,2/3、3/8、-5/9等都是有理数。
数轴是理解有理数和无理数概念的重要工具。在数轴上,每一个点都对应着一个实数(包括有理数和无理数)。有理数在数轴上的分布是稠密的,即任意两个有理数之间都存在无数个其他的有理数。然而,尽管有理数在数轴上看起来是“填满”了整个空间,但实际上它们并不能覆盖所有的实数。这是因为无理数(如π、e、√2等)也存在于数轴上,并且它们与有理数一样,都是实数的一部分。
在数轴上表示有理数时,我们可以利用分数形式或小数形式来确定其位置。例如,要表示有理数1/2,我们可以在数轴上找到0和1的中点;要表示有理数0.75,我们可以从0点出发,向右移动0.75个单位长度。
有理数具有一些重要的性质,这些性质在数学运算和问题解决中发挥着关键作用。
1. 封闭性:有理数在加、减、乘、除(除数不为0)运算下是封闭的,即两个有理数进行这些运算后,结果仍然是有理数。
2. 有序性:有理数之间可以比较大小,即它们满足大小关系(如>、<、=)的传递性、反射性和反对称性。
3. 稠密性:任意两个有理数之间都存在无数个其他的有理数。这一性质使得有理数在数轴上看起来是连续的,但实际上它们并不是连续的(因为无理数的存在)。
4. 阿基米德性质:对于任意两个有理数a和b(a
为了更好地理解有理数的概念,我们
查看全部
相关推荐