
在数学的浩瀚宇宙中,有一个既平凡又神奇的概念,它如同数字世界的一把钥匙,解锁了无数奥秘与规律,那就是——有理数。想象一下,你正在漫步于一条由无数点构成的直线,这条直线,我们通常称之为数轴。在这条线上,有理数就像是那些可以被精准定位的坐标点,它们以一种既有序又和谐的方式排列着,等待着我们去探索、去理解。

“有理数”这个名字听起来似乎充满了哲理与逻辑,而它的由来,也确实与数的“合理性”有关。在古希腊时期,数学家们开始思考什么样的数能够表示为两个整数的比(即分数形式)。他们发现,诸如1、2、3这样的整数,以及像1/2、3/4这样的分数,都能以一种“合理”的方式表达,因为它们都可以写成两个整数的比。于是,这些能够表示为两个整数之比的数,就被称为“有理数”。
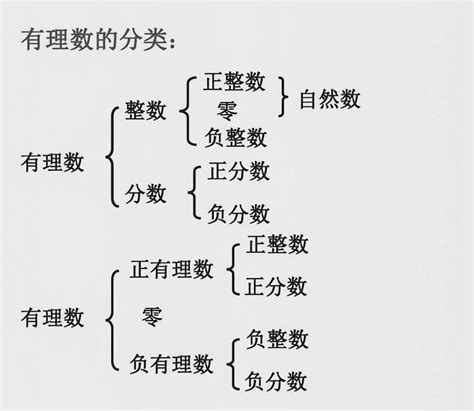
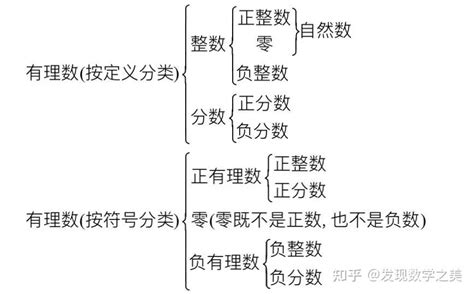
具体地说,有理数定义为可以表示为两个整数a和b(b≠0)之比的数,记作a/b。这里的a是分子,b是分母。例如,3可以看作3/1,而-2/3则直接是一个有理数的例子。有理数包括了所有的整数、有限小数和无限循环小数。值得注意的是,虽然无限不循环小数(如π、e等)在数学中同样重要,但它们却不属于有理数的范畴,而是归属于无理数。
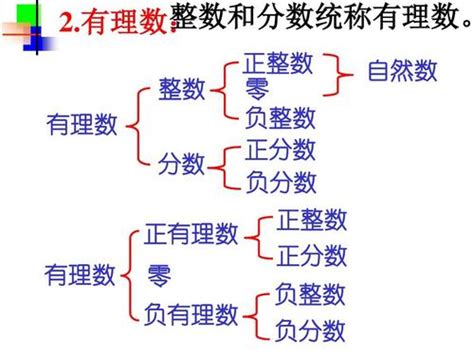
有理数家族庞大而有序,我们可以根据它们与0的关系,将其分为正有理数、0和负有理数三类。正有理数是大于0的有理数,如1/2、3等;0则是有理数中的特殊成员,它既不大于0也不小于0;负有理数则是小于0的有理数,如-1、-2/3等。
有理数还具有一系列重要的性质,这些性质不仅帮助我们理解有理数的行为,也是进行数学运算的基础。
1. 封闭性:任意两个有理数进行加、减、乘、除(除数不为0)运算后,结果仍是有理数。这意味着有理数集在四则运算下是封闭的。
2. 有序性:有理数之间可以比较大小,存在一个明确的顺序关系。这使得我们可以在有理数集上进行排序、寻找最大值或最小值等操作。
3. 稠密性:在任意两个不相等的有理数之间,总可以找到无限多个其他的有理数。这意味着有理数在数轴上分布得极为密集,几乎无处不在。
4. 阿基米德性质:对于任意两个正有理数a和b,总存在一个自然数n,使得na>b。这个性质体现了有理数在数量上的“无限可分”性。
有理数的表示方式多种多样,除了最直接的分数形式外,还可以通过有限小数或无限循环小数来表示。例如,1/4可以表示为0.25(有限小数),而1/3则表示为0.333…(无限循环小数)。这两种表示方式虽然形式不同,但在数学上是等价的,它们都精确地指向了数轴上的同一个点。
在进行有理数的运算时,我们需要遵循一定的规则来确保结果的准确性。对于加法与减法,我们通常需要找到两个有理数的最小公倍数作为通分的分母,然后进行分子的加减运算;对于乘法与除法,则可以直接利用分数的乘法与除法法则进行计算。值得注意的是,在进行除法运算时,如果除数为分数,我们通常将其转化为乘法形式(即乘以除数的倒数)来简化计算过程。
有理数不仅仅是一个抽象的数学概念,它在我们的日常生活中也有着广泛的应用。从简单的购物计算(如打折后的价格)、到复杂的工程设计(如精确测量与比例计算),有理数都扮演着不可或缺的角色。
想象一下,当你在超市购买商品时,商品的标价、折扣率以及你最终需要支付的金额,都是基于有理数的计算得出的。同样地,在建筑设计中,设计师需要精确计算各个构件的尺寸与比例,以确保建筑物的结构稳定与美观。这些计算过程同样离不开有理数的支持。
此外,有理数还是科学研究中不可或缺的工具。无论是物理学中的速度、加速度计算,还是化学中的反应速率、浓度计算,都需要用到有理数来进行精确的描述与预测。
有理数不仅是数学基础的重要组成部分,它还与数学的许多其他分支有着密切的联系。在代数学中,有理数是构建多项式、分式等代数结构的基础;在几何学中,有理数可以用于描述点的坐标、线段的长度以及图形的面积等几何量;在数论中,有理数则是研究整数性质与结构的起点。
更有趣的是,有理数还与无理数之间存在着微妙的联系。无理数虽然无法表示为两个整数的比,但它们却可以通过
查看全部
相关推荐