
在数学的世界里,因数和倍数是两个既相互关联又各具特色的概念。它们如同数学海洋中的两颗璀璨明珠,虽然同属于数论的范畴,但在定义、性质、应用及思维方式上都各有千秋。本文将从多个维度深入探讨因数和倍数的区别,帮助读者更好地理解和区分这两个概念。

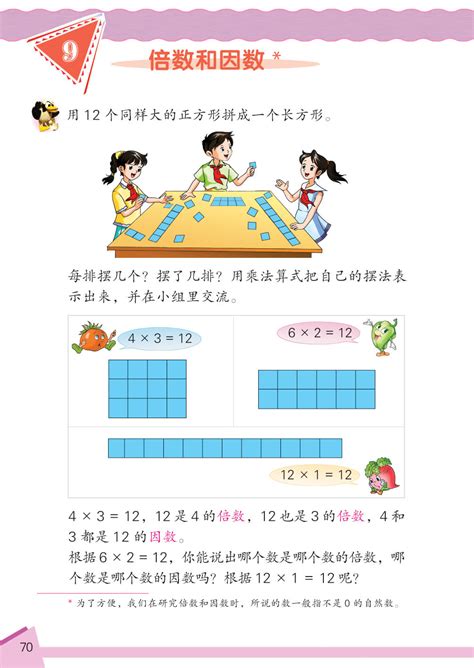
首先,我们从最基础的定义入手。因数,顾名思义,是指能够整除给定数的整数。换句话说,如果整数a能被整数b整除(b≠0),那么我们就说b是a的因数。例如,对于数字12,它的因数有1、2、3、4、6和12本身。值得注意的是,因数总是成对出现的(除了完全平方数的平方根),如1和12、2和6、3和4都是12的因数对。
相比之下,倍数的概念则更加直观。倍数是指一个数能够被另一个数整除而不留余数的结果。具体来说,如果a是b的倍数,那么存在一个整数c,使得a=b×c。以数字3为例,它的倍数有3、6、9、12……等,即任何能被3整除的数都是3的倍数。
从定义上可以看出,因数和倍数的出发点不同:因数关注的是能够整除给定数的那些数,而倍数则是给定数能够整除或作为其乘积结果的那些数。这种本质属性的差异构成了两者区别的基础。
进一步深入,我们可以发现因数和倍数在性质上也存在显著的差异。
因数具有有限性和对称性。对于任何一个正整数n(n>1),它的因数总是有限的,且因数之间可以互换位置而不改变其作为因数的身份,这体现了因数的对称性。此外,因数还遵循着乘积法则,即两个数的乘积的因数可以由这两个数的因数通过乘法组合得到。
倍数则展现出无限性和传递性。对于一个给定的数,它的倍数有无数个,因为只要不断增大乘数c,就可以得到无数个新的倍数。同时,倍数还具有传递性,即如果a是b的倍数,b是c的倍数,那么a也一定是c的倍数。这种性质使得倍数在数列和数轴上形成了一个连续的、无限的序列。
因数和倍数在解决实际问题时也有着不同的应用场景和策略。
在因数的应用方面,我们常常利用因数的性质来解决诸如分解质因数、约数个数计算、最大公约数和最小公倍数求解等问题。例如,在密码学中,质因数分解是加密算法的核心;在几何学中,利用因数的性质可以设计美丽的分形图案;在日常生活中,我们也可以通过计算最大公约数来优化资源分配或计算最小成本。
倍数的应用则更加广泛,它涉及到数列的生成、周期问题的求解、整除性判断等多个方面。例如,在数列中,我们可以利用倍数的性质快速找出某个数列中所有满足特定条件的项;在周期问题中,通过分析倍数关系可以确定事件的重复周期;在整除性判断上,倍数更是判断一个数是否能被另一个数整除的直接依据。
因数和倍数的差异还体现在它们对逻辑推理和问题解决能力的影响上。
在处理因数相关的问题时,我们需要具备一种“分解”的思维,即将复杂的数学问题拆解成更简单的部分,通过寻找和分析因数的关系来解决问题。这种思维方式要求我们具备敏锐的观察力和严谨的逻辑推理能力,能够准确地识别出隐藏在复杂问题背后的因数结构。
而解决倍数问题则需要我们具备一种“扩展”的思维,即从已知的信息出发,通过倍数关系将问题扩展到更广泛的领域或更大的范围。这种思维方式强调的是对信息的灵活运用和逻辑推理的连贯性,要求我们能够在复杂的数学关系中找到倍数关系的线索并据此进行推理。
最后,从教育的角度来看,因数和倍数的学习对于提升学生的数学素养具有重要意义。
因数的学习有助于学生掌握基本的数学概念和技能,如质数与合数的区分、约数的计算等。这些概念和技能是进一步学习数学的基础,也是培养学生逻辑推理能力和问题解决能力的重要途径。
倍数的学习则更多地侧重于培养学生的抽象思维能力和数学应用能力。通过分析和解决倍数相关的问题,学生可以更加深入地理解数学中的整除性、数列和函数等概念,同时学会将数学知识应用于实际问题的解决中。
此外,因数和倍数的学习还能够促进学生的数学交流和合作能力的发展。在解决因数和倍数相关的问题时,学生需要与他人进行交流和讨论,共同探索问题的解决方案。这种交流和合作不仅有助于加深学生对数学知识的理解和掌握,还能够培养他们的团队合作精神和沟通能力。
综上所述,因数和倍数虽然在数学上紧密相连,但在定义、性质、应用及思维方式上都有着明显的差异。通过深入理解和区分这两个概念,我们可以更好地把握数学的本质和规律,提升
查看全部
相关推荐